
We have alreadyy explored False position method and Secant method, now it is time for the simplest method – bisection, also know as interval halving. Methods that uses this theorem are called dichotomy methods, because they divide the interval into two parts (which are not necessarily equal). Step by step bisection method procedure is also given in the article.This method is based on the intermediate value theorem for continuous functions, which says that any continuous function f (x) in the interval that satisfies f (a) * f (b) < 0 must have a zero in the interval. The article discusses all the important points related to the bisection method such as its advantages, disadvantages and solved problems etc. This means that the value that approximates best the root of the function f is the last value of c = 3.1611328.īy solving our quadratic equations in a classic way, we can check our result: The value of f(c) after 9 iterations is less than our defined tolerance (0.0072393 < 0.01). This means that between these points, the plot of the function will cross the x-axis at a particular point, which is the root we need to find. After evaluation of the function in both points, we find that f(a) is positive while f(b) is negative.

The calculation of the value is described below in the table:Īt initialization (i = 0), we choose a = −2 and b = 5. The best way of understanding how the algorithm works are by looking at a bisection method example and solving it by using the bisection method formula.Įxample 1: Find the root of f(x) = 10 − x². It cannot be applied over an interval where the function returns values of the same sign. If the guess interval contains discontinuities, it cannot be used. It is incapable of determining complex roots. Because there are no bracketing values, like f(x) = x². In the case of several roots, the bisection procedure is quick.Īlthough the Bisection method's convergence is guaranteed, it is often slow.Ĭhoosing a guess that is close to the root may necessitate numerous iterations to converge. The bisection method is simple and straightforward to programme on a computer. Each cycle reduces the error bound by 12 per cent. There is a guaranteed error bound in this technique, and it reduces with each repetition. To use the bisection method, we only need to take the average of two values.Įrror bound is guaranteed. There are no complicated calculations required when using the bisection method. Increasing the number of iterations in the bisection method always results in a more accurate root.ĭoesn't demand complicated calculations. The bracketing approach is known as the bisection method, and it is always convergent.Įrrors can be managed. To get the right value with the new value of a or b, we go back to step 2 And recalculate c. We replace b with c if f(c) has the same sign as f(b), and we keep the same value for a We replace a with c if f(c) has the same sign as f(a) and we keep the same value for b If (c) ≠ 0, then we need to check the sign: The root of the function is found only if the value of f(c) = 0. This is called interval halving.Įvaluate the function f for the value of c. Ĭalculate a midpoint c as the arithmetic mean between a and b such that c = (a + b) / 2. Theorem (Bolzano): If on an interval a,b and f(a) So let us understand what Bolzano’s theorem says.

It is based on Bolzano's theorem for continuous functions. It is also known as the Bisection Method Numerical Analysis.

There are various names given to this method such as “ the interval halving method”, “the binary search method”, “the dichotomy method”, and “Bolzano’s Method”.Īs stated above, the Bisection method program is a root-finding method that we often come across while dealing with numerical analysis. This method is based on The Intermediate Value Theorem and is very simple robust and easy to implement.
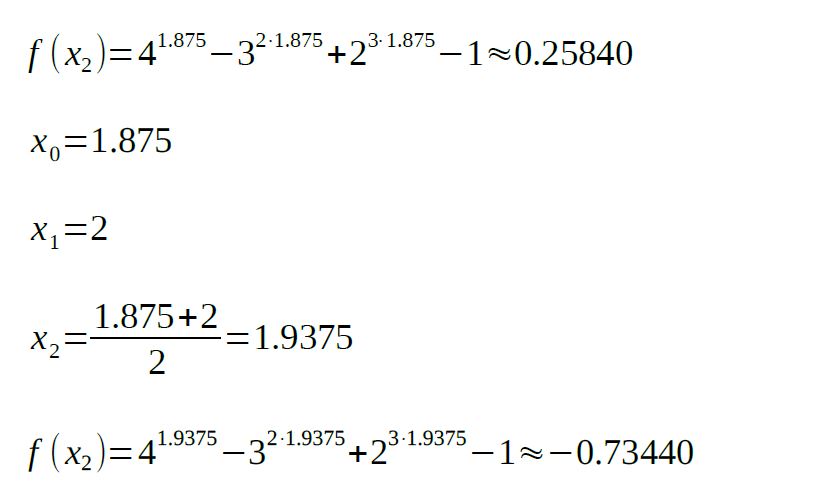
It then successively divides the interval in half and replaces one endpoint with the midpoint so that the root is bracketed. In this method, the interval distance between the initial values is treated as a line segment. For further processing, it bisects the interval and then selects a sub-interval in which the root must lie and the solution is iteratively reached by narrowing down the values after guessing, which encloses the actual solution. In Mathematics, the bisection method is used to find the root of a polynomial function.


 0 kommentar(er)
0 kommentar(er)
